Contoh soal matematika kelas 4 tentang pecahan kurikulum 2013

Memahami Pecahan: Contoh Soal Matematika Kelas 4 Kurikulum 2013

Pecahan adalah salah satu konsep fundamental dalam matematika yang mulai diperkenalkan secara lebih mendalam pada jenjang Sekolah Dasar, khususnya di kelas 4. Berdasarkan Kurikulum 2013 (K-13), pembelajaran pecahan tidak hanya berfokus pada perhitungan semata, melainkan juga pada pemahaman konsep yang kuat, representasi visual, dan aplikasinya dalam kehidupan sehari-hari. Tujuannya adalah agar siswa mampu berpikir logis, kritis, dan kreatif dalam menyelesaikan masalah yang melibatkan pecahan.

Artikel ini akan mengupas tuntas konsep pecahan yang diajarkan di kelas 4 K-13, dilengkapi dengan berbagai contoh soal dan pembahasannya. Diharapkan, artikel ini dapat menjadi panduan bagi guru, orang tua, dan siswa dalam memahami serta menguasai materi pecahan.

I. Konsep Pecahan dalam Kurikulum 2013 Kelas 4

Kurikulum 2013 menekankan pendekatan saintifik yang melibatkan pengamatan, menanya, mencoba, menalar, dan mengomunikasikan. Dalam konteks pecahan, siswa diajak untuk:

1. Memahami Makna Pecahan: Pecahan sebagai bagian dari keseluruhan, bagian dari kumpulan, dan posisi pada garis bilangan.
2. Mengidentifikasi Pecahan Senilai: Pecahan yang memiliki nilai yang sama meskipun pembilang dan penyebutnya berbeda.
3. Membandingkan Pecahan: Menentukan apakah suatu pecahan lebih besar dari, lebih kecil dari, atau sama dengan pecahan lain.
4. Menjumlahkan dan Mengurangkan Pecahan Berpenyebut Sama: Operasi dasar pecahan dengan penyebut yang identik.
5. Menyelesaikan Masalah Kontekstual: Mengaplikasikan pemahaman pecahan dalam situasi nyata sehari-hari.

Pembelajaran dimulai dengan menggunakan media konkret atau visual (misalnya, potongan buah, pizza, kertas lipat) untuk membantu siswa memahami konsep abstrak pecahan sebelum beralih ke representasi simbolik.

II. Contoh Soal dan Pembahasan

Mari kita bedah berbagai jenis contoh soal pecahan yang relevan untuk siswa kelas 4. Setiap contoh soal akan dilengkapi dengan pembahasan langkah demi langkah dan penekanan pada konsep yang terkait.

A. Konsep Dasar Pecahan (Pecahan sebagai Bagian dari Keseluruhan/Kumpulan)

Soal 1:
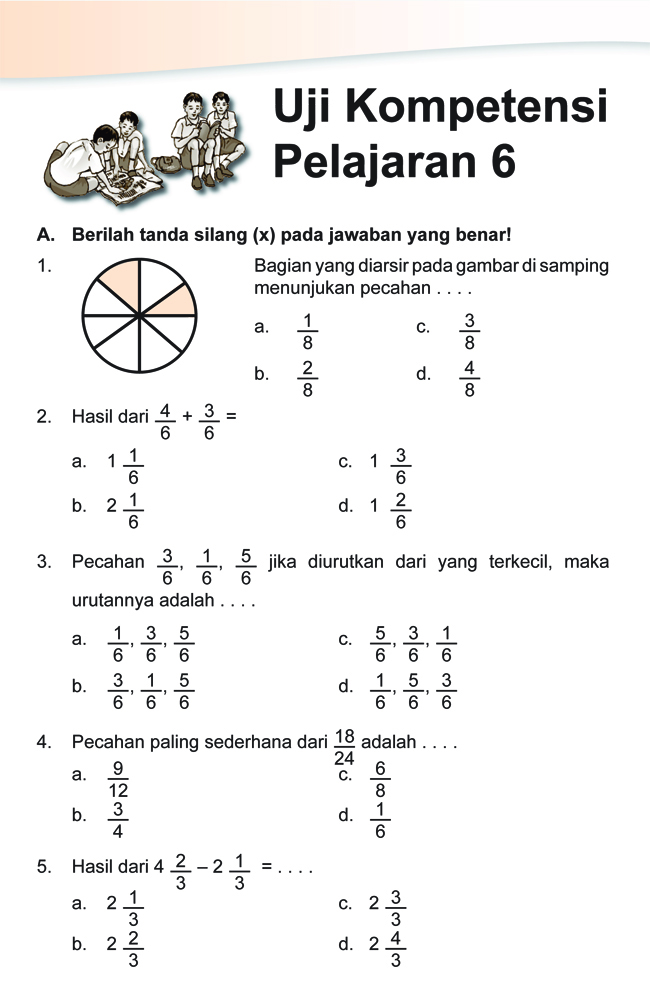
Perhatikan gambar berikut! Sebuah lingkaran dibagi menjadi 8 bagian sama besar, dan 3 bagian di antaranya diarsir.
(Anggap ada gambar lingkaran dengan 8 bagian, 3 diarsir)
Berapa nilai pecahan yang menyatakan bagian yang diarsir?

Pembahasan:

• Langkah 1: Hitung jumlah seluruh bagian yang sama besar pada lingkaran. Ada 8 bagian. Ini akan menjadi penyebut (angka di bawah garis pecahan).
• Langkah 2: Hitung jumlah bagian yang diarsir. Ada 3 bagian. Ini akan menjadi pembilang (angka di atas garis pecahan).
• Langkah 3: Gabungkan pembilang dan penyebut.

Jawaban: Nilai pecahan yang menyatakan bagian yang diarsir adalah 3/8.

Konsep Terkait: Pecahan sebagai bagian dari keseluruhan. Pembilang menunjukkan bagian yang diamati, penyebut menunjukkan jumlah keseluruhan bagian yang sama besar.

Soal 2:
Ibu memiliki 10 buah apel. Sebanyak 4 apel berwarna merah, dan sisanya berwarna hijau. Berapa pecahan yang menyatakan bagian apel berwarna merah dari seluruh apel?

Pembahasan:

• Langkah 1: Tentukan jumlah seluruh apel. Ada 10 apel. Ini adalah penyebut.
• Langkah 2: Tentukan jumlah apel berwarna merah. Ada 4 apel. Ini adalah pembilang.
• Langkah 3: Bentuk pecahan dari informasi tersebut.

Jawaban: Pecahan yang menyatakan bagian apel berwarna merah adalah 4/10.

Konsep Terkait: Pecahan sebagai bagian dari kumpulan objek.

Soal 3:
Gambarkan garis bilangan dan tunjukkan posisi pecahan 2/5 pada garis bilangan tersebut.

Pembahasan:

• Langkah 1: Buat garis bilangan. Beri tanda 0 di ujung kiri dan 1 di ujung kanan.
• Langkah 2: Perhatikan penyebut pecahan, yaitu 5. Artinya, kita harus membagi ruas garis dari 0 sampai 1 menjadi 5 bagian yang sama besar.
• Langkah 3: Hitung 2 langkah dari 0 ke kanan untuk menemukan posisi 2/5.

Jawaban:

0 ---|---|---|---|--- 1
    1/5 2/5 3/5 4/5
    ^
    Posisi 2/5

Konsep Terkait: Representasi pecahan pada garis bilangan.

B. Pecahan Senilai

Soal 4:
Tentukan dua pecahan yang senilai dengan 1/3.

Pembahasan:
Pecahan senilai diperoleh dengan mengalikan atau membagi pembilang dan penyebut dengan bilangan yang sama (selain nol).

• Cara 1 (Mengalikan dengan 2):
  (1 × 2) / (3 × 2) = 2/6
• Cara 2 (Mengalikan dengan 3):
  (1 × 3) / (3 × 3) = 3/9

Jawaban: Dua pecahan yang senilai dengan 1/3 adalah 2/6 dan 3/9. (Bisa juga 4/12, 5/15, dst.)

Konsep Terkait: Pecahan senilai. Prinsip perkalian yang sama pada pembilang dan penyebut.

Soal 5:
Apakah pecahan 2/4 senilai dengan 3/6? Jelaskan!

Pembahasan:
Kita bisa mengecek kesetaraan pecahan dengan beberapa cara:

• Cara 1 (Menyederhanakan Pecahan):

  • Sederhanakan 2/4: Bagi pembilang dan penyebut dengan 2. 2 ÷ 2 = 1, 4 ÷ 2 = 2. Jadi, 2/4 = 1/2.
  • Sederhanakan 3/6: Bagi pembilang dan penyebut dengan 3. 3 ÷ 3 = 1, 6 ÷ 3 = 2. Jadi, 3/6 = 1/2.
    Karena keduanya sama-sama setara dengan 1/2, maka 2/4 senilai dengan 3/6.

• Cara 2 (Perkalian Silang):
  Kalikan pembilang pecahan pertama dengan penyebut pecahan kedua, dan pembilang pecahan kedua dengan penyebut pecahan pertama.
  2/4 dan 3/6
  (2 × 6) = 12
  (3 × 4) = 12
  Karena hasil perkalian silangnya sama (12 = 12), maka pecahan tersebut senilai.

Jawaban: Ya, pecahan 2/4 senilai dengan 3/6.

Konsep Terkait: Pecahan senilai, penyederhanaan pecahan, dan pengujian kesetaraan pecahan.

C. Membandingkan Pecahan

Soal 6:
Isilah titik-titik dengan tanda < (lebih kecil dari), > (lebih besar dari), atau = (sama dengan):
a. 1/4 … 3/4
b. 2/5 … 2/3

Pembahasan:
a. 1/4 … 3/4

• Jika penyebutnya sama, bandingkan saja pembilangnya. Angka pembilang yang lebih besar menunjukkan pecahan yang lebih besar.

• 1 < 3.

  Jawaban a: 1/4 < 3/4

b. 2/5 … 2/3

• Jika pembilangnya sama, bandingkan penyebutnya. Pecahan dengan penyebut yang lebih kecil (artinya dibagi menjadi bagian yang lebih sedikit tapi lebih besar) akan memiliki nilai yang lebih besar.

• Pikirkan pizza: 2 dari 5 potong vs 2 dari 3 potong. 2 dari 3 potong lebih besar.

  Jawaban b: 2/5 < 2/3

Konsep Terkait: Membandingkan pecahan berpenyebut sama dan berpembilang sama.

Soal 7:
Urutkan pecahan berikut dari yang terkecil hingga terbesar: 1/2, 1/4, 3/4.

Pembahasan:

• Langkah 1: Perhatikan penyebutnya. Ada 2 dan 4. Untuk membandingkan, sebaiknya samakan penyebutnya. Kelipatan persekutuan terkecil (KPK) dari 2 dan 4 adalah 4.
• Langkah 2: Ubah 1/2 agar memiliki penyebut 4.
  1/2 = (1 × 2) / (2 × 2) = 2/4
• Langkah 3: Sekarang semua pecahan memiliki penyebut yang sama: 2/4, 1/4, 3/4.
• Langkah 4: Urutkan berdasarkan pembilangnya dari yang terkecil.
  1/4, 2/4, 3/4

Jawaban: Urutan pecahan dari yang terkecil adalah 1/4, 1/2, 3/4.

Konsep Terkait: Membandingkan pecahan dengan penyebut berbeda (dengan menyamakan penyebut).

D. Penjumlahan dan Pengurangan Pecahan Berpenyebut Sama

Soal 8:
Hitunglah hasil dari 2/7 + 3/7.

Pembahasan:

• Langkah 1: Periksa penyebutnya. Keduanya adalah 7, jadi sudah sama.
• Langkah 2: Jumlahkan hanya pembilangnya.
  2 + 3 = 5
• Langkah 3: Penyebut tetap sama.

Jawaban: 2/7 + 3/7 = 5/7.

Konsep Terkait: Penjumlahan pecahan berpenyebut sama.

Soal 9:
Andi memiliki kue cokelat sebanyak 5/6 bagian. Ia memakan 2/6 bagian dari kue tersebut. Berapa sisa kue Andi sekarang?

Pembahasan:
Ini adalah soal pengurangan pecahan.

• Langkah 1: Tuliskan operasi pengurangannya: 5/6 – 2/6.
• Langkah 2: Periksa penyebutnya. Keduanya adalah 6, jadi sudah sama.
• Langkah 3: Kurangkan hanya pembilangnya.
  5 – 2 = 3
• Langkah 4: Penyebut tetap sama.
  Hasilnya adalah 3/6.
• Langkah 5 (Opsional tapi penting): Sederhanakan pecahan jika memungkinkan.
  3/6 dapat disederhanakan dengan membagi pembilang dan penyebut dengan 3.
  3 ÷ 3 = 1
  6 ÷ 3 = 2
  Jadi, 3/6 = 1/2.

Jawaban: Sisa kue Andi sekarang adalah 3/6 atau 1/2 bagian.

Konsep Terkait: Pengurangan pecahan berpenyebut sama, penyederhanaan pecahan.

E. Soal Cerita Aplikasi Pecahan

Soal 10:
Lina memiliki pita sepanjang 3/4 meter. Ia menggunakan 1/4 meter pita untuk menghias kado. Berapa panjang sisa pita Lina sekarang?

Pembahasan:

• Identifikasi: Ini adalah masalah pengurangan. Panjang awal pita dikurangi panjang yang digunakan.
• Operasi: 3/4 – 1/4
• Penyelesaian: Karena penyebutnya sama (4), kita hanya perlu mengurangi pembilangnya.
  3 – 1 = 2
  Penyebut tetap 4. Jadi hasilnya 2/4.
• Sederhanakan: Pecahan 2/4 dapat disederhanakan dengan membagi pembilang dan penyebut dengan 2.
  2 ÷ 2 = 1
  4 ÷ 2 = 2
  Hasil sederhana adalah 1/2.

Jawaban: Panjang sisa pita Lina sekarang adalah 1/2 meter.

Konsep Terkait: Penerapan pengurangan pecahan dalam soal cerita, penyederhanaan pecahan.

Soal 11:
Ayah membeli sebuah pizza dan memotongnya menjadi 8 bagian sama besar. Kakak makan 3 potong dan adik makan 2 potong. Berapa bagian pizza yang sudah dimakan oleh kakak dan adik seluruhnya?

Pembahasan:

• Identifikasi: Ini adalah masalah penjumlahan. Bagian pizza yang dimakan kakak ditambah bagian yang dimakan adik.
• Representasi Pecahan:
  • Kakak makan 3 potong dari 8 = 3/8
  • Adik makan 2 potong dari 8 = 2/8
• Operasi: 3/8 + 2/8
• Penyelesaian: Karena penyebutnya sama (8), kita hanya perlu menjumlahkan pembilangnya.
  3 + 2 = 5
  Penyebut tetap 8. Jadi hasilnya 5/8.

Jawaban: Bagian pizza yang sudah dimakan oleh kakak dan adik seluruhnya adalah 5/8 bagian.

Konsep Terkait: Penerapan penjumlahan pecahan dalam soal cerita.

III. Tips untuk Mengajarkan Pecahan di Kelas 4 (Kurikulum 2013)

Untuk memastikan siswa menguasai konsep pecahan dengan baik, beberapa tips berikut dapat diterapkan:

1. Gunakan Media Konkret dan Visual: Awalilah pembelajaran dengan benda-benda nyata yang mudah dibagi (kue, buah, kertas lipat, lego). Setelah itu, beralihlah ke gambar dan diagram. Visualisasi sangat membantu siswa memahami makna pecahan.
2. Kaitkan dengan Kehidupan Sehari-hari: Buatlah soal cerita yang relevan dengan pengalaman siswa (misalnya, berbagi makanan, mengukur bahan, jarak tempuh). Ini membuat matematika terasa lebih bermakna.
3. Fokus pada Pemahaman Konsep, Bukan Hanya Prosedur: Jangan terburu-buru mengenalkan rumus. Pastikan siswa memahami mengapa 1/2 sama dengan 2/4, atau mengapa penyebut tidak dijumlahkan saat operasi penjumlahan.
4. Latihan Bervariasi: Berikan berbagai jenis soal, mulai dari identifikasi, membandingkan, operasi dasar, hingga soal cerita.
5. Perkuat Konsep Pecahan Senilai: Pemahaman pecahan senilai adalah kunci untuk operasi pecahan yang lebih kompleks di jenjang selanjutnya (misalnya, penjumlahan/pengurangan pecahan berpenyebut tidak sama).
6. Gunakan Garis Bilangan: Garis bilangan adalah alat visual yang sangat efektif untuk membandingkan pecahan dan menunjukkan posisi pecahan.
7. Sabar dan Apresiatif: Pembelajaran pecahan bisa jadi menantang bagi sebagian siswa. Berikan dukungan penuh, dorong mereka untuk bertanya, dan berikan apresiasi atas setiap usaha dan kemajuan.

IV. Penutup

Pecahan adalah pintu gerbang menuju pemahaman konsep matematika yang lebih kompleks. Dengan fondasi yang kuat di kelas 4, siswa akan lebih siap menghadapi materi pecahan di jenjang berikutnya, seperti pecahan campuran, desimal, persentase, serta operasi perkalian dan pembagian pecahan. Kurikulum 2013 telah membimbing kita untuk mengajarkan pecahan secara kontekstual dan bermakna. Dengan latihan yang konsisten dan pendekatan yang tepat, setiap siswa dapat menguasai pecahan dengan percaya diri dan menjadikan matematika sebagai pelajaran yang menyenangkan.

Semoga artikel ini bermanfaat sebagai panduan dalam mendampingi putra-putri atau peserta didik Anda belajar pecahan. Selamat belajar!

(Catatan: Gambar lingkaran pada Soal 1 hanya sebagai placeholder teks, Anda bisa menyisipkan gambar sebenarnya jika artikel ini akan dipublikasikan secara visual.)